점성이 없고 유체의 밀도가 압력에 따라 변하는 압축성 유체의 경우, 유체 변수의 초기조건 및 경계조건, 그리고 유체가 흐르는 영역의 기하학적 성질에 따라 유체 변수가 연속적 또는 불연속적으로 변합니다. 본 과제의 궁극적인 연구 목표는 비점성 압축성 유체에서 발생하는 충격파와 관련된 오래된 두 개의 난제를 해결하는 것입니다.

— 주제 1

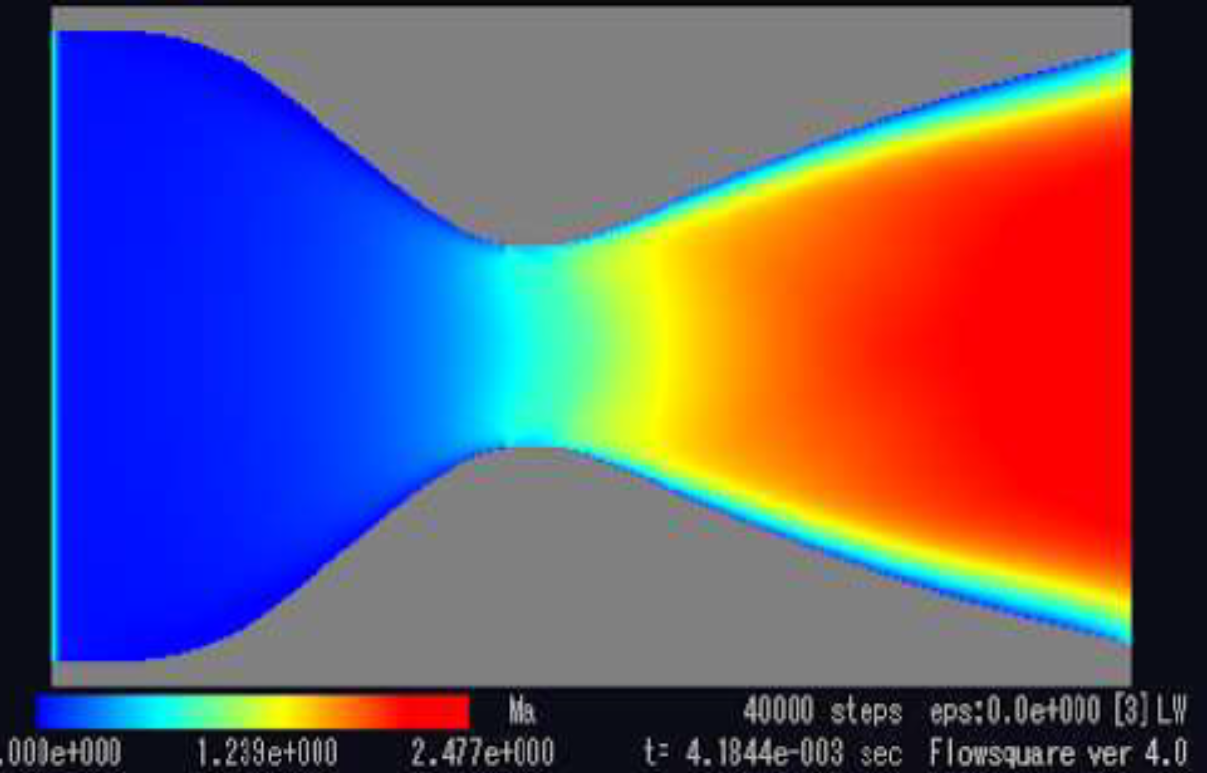
De Laval nozzle문제: 유체가 흐르는 영역의 단면적이 유체의 주요 운동방향에 따라 감소하다가 일정 지점에서 다시 증가하는 수렴형-발산형 노즐에서 유체가 가속을 하다가 속력이 음속을 돌파하여 초음속(supersonic) 상태가 되었다가, 천음속(transonic) 충격파가 발생한 후 다시 아음속(subsonic) 상태로 급격하게 변하는 현상은 관측과 실험을 통해서 잘 알려져 있습니다 (그림1). 그러나, 이 현상의 구조적 역학적 안정성에 대한 정확한 이론은 아직까지 알려진 바가 없습니다.

본 과제에서, 이온화된 기체의 운동을 기술하는 오일러-포아송 방정식(Euler-Poisson equations)시스템을 연구하여, De Laval nozzle에서 발생하는 현상과 유사한 천음속 변이현상에 대한 수학적 분석을 하고, 이를 바탕으로 궁극적으로 De Laval nozzle문제의 해결에 도전하는 것이 목표입니다.

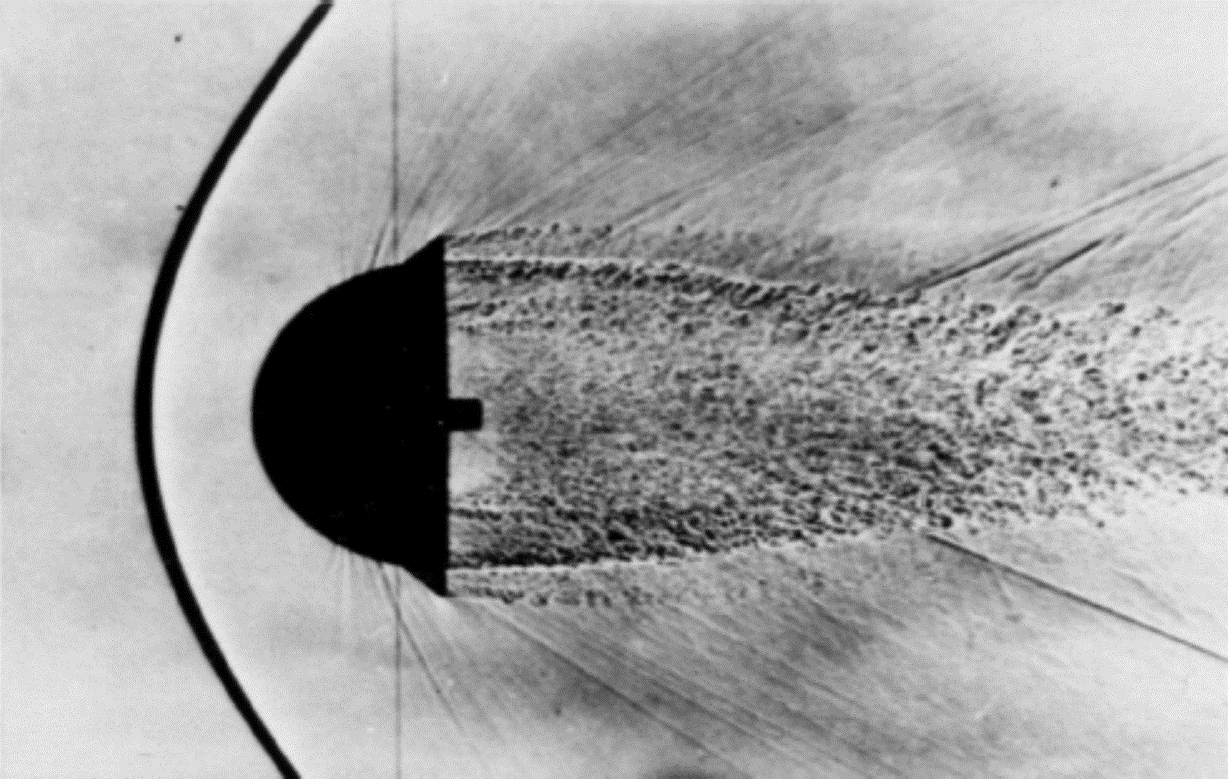
그림1. Transonic flow in a de Laval nozzle	그림2. Detached shock past a blunt body

* 그림 출처: http://flowsquare.com/2013/12/24/de-laval-nozzle/,  http://www.hq.nasa.gov/office/pao/History/SP-440/ch6-2.htm

— 주제 2

끝이 뭉툭한 발사체(Blunt body)가 초음속으로 비행할 때 발생하는 분리 충격파 (detached shock) 현상은 로켓발사 또는 전투기가 음속을 돌파하여 비행할 때 종종 관측됩니다 (그림2), 이러한 분리 충격파의 발생은 운동체의 비행의 안정성에 큰 영향을 끼치므로, 분리 충격파 현상이 동체의 기하학적 구조에 따라 어떻게 발생하는 지를 정확히 이해하는 것은 매우 중요한데 지금까지 알려진 대부분의 연구는 실험에 바탕을 둔 근사 이론(approximation theory)에 불과합니다. 그러나 충격파 현상은 기체 운동의 비선형적인 성질에 의해 발생하므로, 근사 이론으로 현상을 정확하게 이해하는 것에는 한계가 있습니다.

본 과제에서는 비행체가 특정 구조를 가질 때 발생하는 분리 충격파를 비선형 편미분방정식 시스템의 분석을 통해 이해하고, 이를 근거로 정확한 이론을 수립하고자 합니다.

위에서 설명한 두 개의 오래된 난제를 연구함에 있어서 초점을 두는 부분은 바로 유체의 국소 회전도(vorticity)가 어떻게 충격파 현상에 영향을 끼치는지를 이해하는 것입니다. 다차원 유체운동에 대한 연구결과 중 대부분은 회전도가 0인 상태에 대한 것입니다. 그러나, 충격파가 발생하면 충격파 단면에서 엔트로피의 변이가 발생하고 이에 따라 자연스럽게 회전도가 발생하게 됩니다. 그러므로, 기존의 연구결과로 충격파 현상을 설명하는 것은 어렵습니다. 이러한 한계를 극복하기 위해, 헬름홀츠 분해법(Helmholtz decomposition)을 이용하여 회전도가 0이 아닌 기체운동 방정식 시스템을 연구하고, 이를 통해 충격파 현상의 정확한 이론 수립에 기여할 것입니다.

※ 헬름홀츠 분해법: 유체의 속도벡터를 압축성과 회전도 부분으로 분해해서 각각의 특성 및 기여도를 파악할 수 있는 기법